이분 탐색트리란?
보통 우리가 어떤 걸 탐색하기 위해서 list 혹은 배열에 안에 있는것들을 순차적으로 방문하면서
데이터를 찾았다. 하지만 이 방법은 데이터의 양이 많을때 해당 방법을 사용하면 시간 복잡도가 커질수가 있다.
하지만 이분 탐색은 정렬되어 있는 정렬되어 있는 리스트에서 탐색 범위를 절반씩 감소시키는것이다.
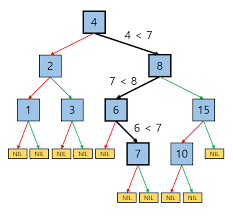
따라서 데이터 가 많은 곳에서의 특정 데이터를 빠르게 검색하려면 이진 탐색을 사용하는것이 맞다.
하지만 위에서 언급했듯이 정렬되어 있는 리스트에서만 사용할수 있기 때문에
특정 상황에서는 사용하지 못할수도 있다.
이분 탐색의 알고리즘의 과정
상황 : 배열 {0,1,2,3,4,5,6,7,8,9} 에서 숫자 2를 찾으려고 한다.
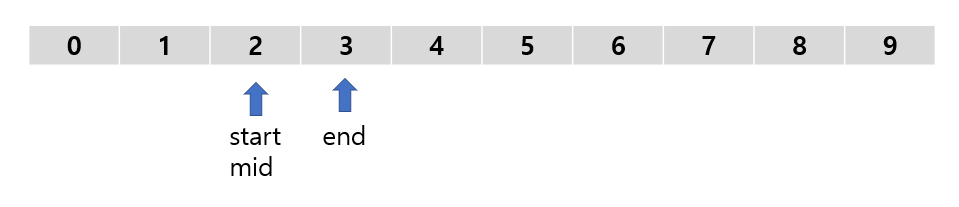
1. 정렬된 배열(혹은 list)에서 start와 end index 를 정하고 (start + end)/2를 통해서 mid index를 구한다.

2. 찾으려는 수 2가 mid보다 작으니 start와 end index를
start = start, end = mid - 1 로 수정을 한다음 받은 start index와 end index를 통해서 mid index를 구한다.

3. 찾으려는 수 2가 mid보다 크니 start 와 end index를
start = mid+1 , end = end 로 수정을 한다음 mid index를 구한다.
4. 찾으려는 수 2가 mid와 같으니 데이터를 찾고 return 하게 된다.
위와 같은 과정을 통해서 우리가 찾으려는 수를 찾게 된다.
우리가 이분탐색을 구현을 하려면 배열을 이진트리로 구현을 할줄 알아야 한다.
그래서 소스로 이분탐색을 구현하기에 앞서 우리는 배열을 통해서 이진트리를 구현을 해보자.
BinaryTree Class
package co.kr.wook;
public class BinaryTree{
//트리를
class Node {
int data; //node 숫자를 저장하는 변수
Node leftNode; //data보다작은 node를 담는 변수
Node rightNode;//data 보다 큰 node를 담는 변수
public Node(int data) {
this.data = data;
}
}
Node root;
public void makeTree(int[] arr) {
root = makeTree(arr,0,arr.length-1);
}
public Node makeTree(int[] arr, int start, int end) {
if(start> end) //start가 크다면 out, 재귀호출을 끝내는 지점
return null;
int mid = (start+end)/2;
Node node = new Node(arr[mid]);
node.leftNode = makeTree(arr,start,mid-1); //중간지점 보다 작은 node를 재귀호출로 담음
node.rightNode = makeTree(arr,mid+1,end); //중간지점보다 큰 node를 재귀호출로 담음
return node;
}
}main 함수
public static void main(String[] args) {
// TODO Auto-generated method stub
PreTest p = new PreTest();
int[] numbers = new int[10];
for(int i = 0; i<numbers.length;i++) {
numbers[i] = i;
}
BinaryTree bt = new BinaryTree();
bt.makeTree(numbers);
}
해당 소스가 이해가 가지 않는다면 직접 손코딩 해보는것을 추천한다.

위 그림은 내가 직접 손코딩한 결과다ㅋㅋㅋㅋㅋㅋ
아직 재귀호출에 익숙치 않아 손코딩을 어느정도 하지 않으면 이해가 가질 않는다.
하지만 하다보면 아 이런식으로 되는구나를 알수 있다.
무튼 위 소스로 이진 트리를 했다면 이제 검색하는것은 메소드 하나만 추가하면 된다.
소스는 아래와 같다.
BinaryTree Class
public class BinaryTree{
class Node {
int data;
Node leftNode;
Node rightNode;
public Node(int data) {
this.data = data;
}
}
Node root;
public void makeTree(int[] arr) {
root = makeTree(arr,0,arr.length-1);
}
public Node makeTree(int[] arr, int start, int end) {
if(start> end)
return null;
int mid = (start+end)/2;
Node node = new Node(arr[mid]);
node.leftNode = makeTree(arr,start,mid-1);
node.rightNode = makeTree(arr,mid+1,end);
return node;
}
public void searchBTree(Node node, int find) {
if(find<node.data) {
System.out.println("찾으려는 데이터가 "+node.data+"보다 작음");
searchBTree(node.leftNode,find);
}else if(find>node.data) {
System.out.println("찾으려는 데이터가 "+node.data+"보다 큼");
searchBTree(node.rightNode,find);
}else {
System.out.println("찾았당");
}
}
}
main 함수
public static void main(String[] args) {
// TODO Auto-generated method stub
PreTest p = new PreTest();
int[] numbers = new int[10];
for(int i = 0; i<numbers.length;i++) {
numbers[i] = i;
}
BinaryTree bt = new BinaryTree();
bt.makeTree(numbers);
bt.searchBTree(bt.root, 2);
}
수슬 찾는것도 재귀호출을 통해서 수를 찾도록 했다.
'코딩일기 > 알고리즘' 카테고리의 다른 글
| [프로그래머스 : 레벨 4] 징검다리 : 이분탐색(Java) (0) | 2021.07.02 |
|---|---|
| [프로그래머스 : 레벨3] 입국심사 : 이분탐색(Java) (0) | 2021.06.30 |
| [프로그래머스 : 레벨3] 여행경로 : DFS(Java) (0) | 2021.06.22 |
| [프로그래머스 : 레벨 3] 단어변환 : BFS(Java) (0) | 2021.06.21 |
| [프로그래머스 : 레벨 3] 네트워크 : DFS(Java) (0) | 2021.06.21 |