이번 문제는 계단을 연속 3번 오르면 안된다는 제약 조건 때문에 문제를 풀지 못해 답을 보게 되었다.
문제를 살펴보자.
문제
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.
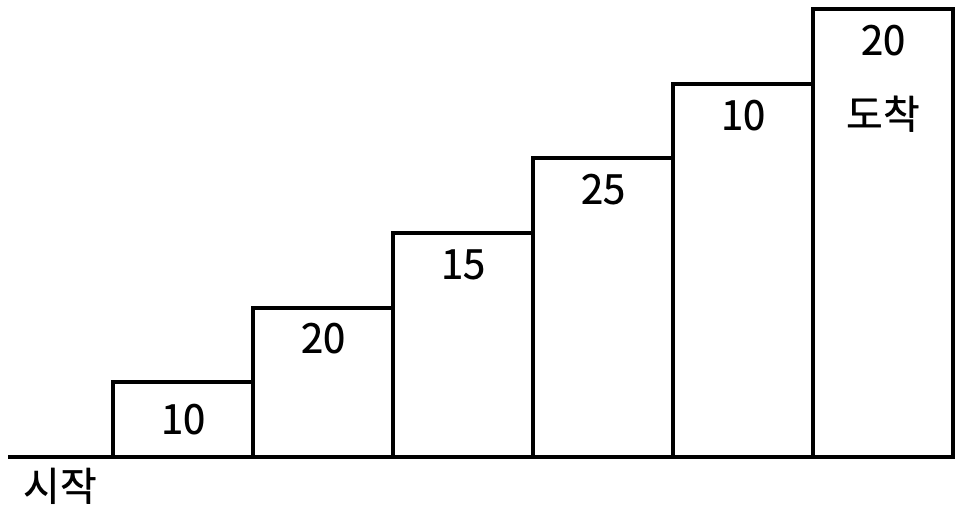
<그림 1>
예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.

<그림 2>
계단 오르는 데는 다음과 같은 규칙이 있다.
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.
각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
입력
입력의 첫째 줄에 계단의 개수가 주어진다.
둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.
출력
첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.

문제 접근 방법
이번 문제는 Top - Down 방식으로 재귀호출하여서 DP를 사용해서 문제를 풀어야 한다.
Top - Down이여야 하는 이유는 문제에서 마지막 계단은 꼭 밟아야 한다는 조건이 붙었기 때문이다.
그래서 Top - Down 방식이여야 한다.
그렇다면 점화식은 어떻게 나와야 할까
점화식을 알아내려면 일단 문제에서 제시한 조건을 잘 확인해봐야 한다.
1. 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다
2. 연속된 세 개의 계단을 모두 밟아서는 안 된다
일단 우리는 해당 계단을 어떻게해서 왔는지를 위의 조건에 맞게 알아봐야 한다.
6번째 계단을 도착하려면
4 -> 6 이렇게 오거나
3 -> 5 -> 6 이렇게 와야 한다.
따라서 우리는 위 두가지 방식중 수가 더 큰 값을 선택해서 값을 넣으면 된다.
그렇담 재귀 식은
아래와 같이 된다.
Math.max(getMax(dp,i-2,stair),getMax(dp,i-3,stair)+stair[i-1]) + stair[i];위 식을 보고 어 그럼 6번째 계단일떄 dp[4],dp[5]+arr[3] 이렇게 하면 되지
왜 Math.max(dp[n-2],dp[n-3]+arr[n-1]) 을 하지 하는 의문점이 들수가 있다.
위 방법처럼 n-1도 재귀호출을 통해서 만들게되면 dp에 저장되는 값이 매번 달라지기때문에 dp의 기능을 잃어
매번 새로운 값을 구해야 한다.
예를 들자면
6 -> 5 -> 3 에서 3에서 올수 있는 계단은 1과 2가 있다.
따라서 3은 1과 2중 큰계단을 밟아 값을 더해 dp[3]의 값을 저장하게 된다. 위 문제대로라면
dp[3] +dp[2]가 된다.
하지만
6 -> 4 ->3으로 갔을땐 이전에 저장된 3의 값으로 갈수가 없다.
왜냐하면 이전에 dp에 저장된 3의 값은 dp[3] + dp[2]가 되어 연속된 3개의 계단을 밟는것이기 때문이다.
따라서 직전의 n-1 값은 기존의 계단값이 저장된 stair[n-1]을 통해서 값을 가져와야 한다.
그래서 위의 내용을 토대로 작성된 전체 코드는 아래와 같다.
import java.util.Scanner;
public class Run {
public static void main(String[] args) {
// TODO Auto-generated method stub
Run a = new Run();
Scanner sc = new Scanner(System.in);
int stairs = sc.nextInt();
int[] stair = new int[stairs];
for(int i = 0; i<stairs;i++) {
stair[i] = sc.nextInt();
}
int[] dp = new int[stairs];
dp[0] = stair[0];
if(stairs >= 2) {
dp[1] = dp[0] + stair[1];
}
System.out.println(a.getMax(dp, stairs-1, stair));
}
public int getMax(int[] dp, int i,int[] stair) {
// TODO Auto-generated method stub
if(i<0) {
return 0;
}
if(dp[i] == 0) { //dp 부분이 비어 있다면 진입
dp[i] = Math.max(getMax(dp,i-2,stair),getMax(dp,i-3,stair)+stair[i-1]) + stair[i];
}
return dp[i];
}
}'코딩일기 > 알고리즘' 카테고리의 다른 글
| [백준 11724번 : 실버2] 연결 요소의 개수 ( DFS / Java) (0) | 2021.08.05 |
|---|---|
| [백준 1946번 : 실버 1] 신입사원 ( 그리디 / Java) (0) | 2021.08.05 |
| [백준 1697번 : 실버1] 숨바꼭질 (BFS / Java) (0) | 2021.07.30 |
| [백준 10162번 :브론즈4] 전자레인지 (그리디/Java) (0) | 2021.07.29 |
| [백준 10870번 : 브론즈2] 피보나치수 5 (DP/ Java) (0) | 2021.07.29 |



