이번 문제는 내가 다른 DFS 알고리즘으로 풀어서 틀려가지고 결국엔 답을 본 문제다.
막상 답을 보니 나도 금방 내 소스에 녹아냈는데 좀더 문제를 자세히 볼걸 하며 약간 아쉬웠던 문제였다.
일단 문제부터 살펴보자.
문제 설명
n개의 노드가 있는 그래프가 있습니다. 각 노드는 1부터 n까지 번호가 적혀있습니다. 1번 노드에서 가장 멀리 떨어진 노드의 갯수를 구하려고 합니다. 가장 멀리 떨어진 노드란 최단경로로 이동했을 때 간선의 개수가 가장 많은 노드들을 의미합니다.
노드의 개수 n, 간선에 대한 정보가 담긴 2차원 배열 vertex가 매개변수로 주어질 때, 1번 노드로부터 가장 멀리 떨어진 노드가 몇 개인지를 return 하도록 solution 함수를 작성해주세요.
제한사항
- 노드의 개수 n은 2 이상 20,000 이하입니다.
- 간선은 양방향이며 총 1개 이상 50,000개 이하의 간선이 있습니다.
- vertex 배열 각 행 [a, b]는 a번 노드와 b번 노드 사이에 간선이 있다는 의미입니다.
입출력 예
| n | vertex | return |
| 6 | [[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]] | 3 |
입출력 예 설명
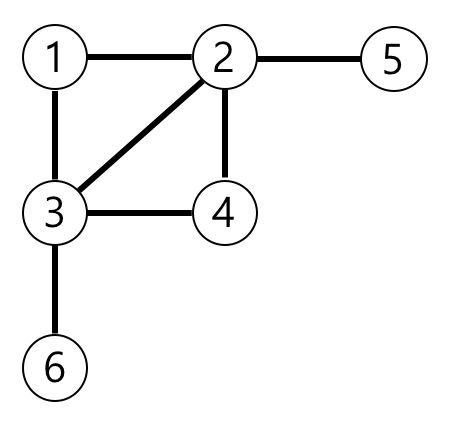
예제의 그래프를 표현하면 아래 그림과 같고, 1번 노드에서 가장 멀리 떨어진 노드는 4,5,6번 노드입니다.
문제 풀이
1. 일단 그래프를 만들어 낸다.
2. 문제에서 최단 경로로 이동했다고 하니 해당 문제는 간선간의 거리는 BFS를 통해서 구한다.
BFS를 안다면 금방 풀수있는 문제가 될것 같다.
BFS에 대한 설명은 아래 링크에 자세히 나와 있으니 확인하면 될거 같다.
https://wpioneer.tistory.com/131?category=1023663
[자료구조] BFS(Breadth First Search) Java 구현
BFS는 Breadth First Search로 너비우선 탐색이란 뜻을 가진다. 너비 우선 탐색을 아래와 같은 과정으로 그래프를 모두 순회하는것이다. 자식노드와 그 형제노드를 모두 검색한뒤 그 다음에 있는 자식
wpioneer.tistory.com
전체적인 소스를 보여주겠다.
public int solution(int n, int[][] edge) {
int answer = 0;
//그래프 구현
LinkedList<Integer>[] graph = new LinkedList[n+1];
for(int i= 0;i<graph.length;i++) {
graph[i] = new LinkedList<Integer>();
}
for(int i = 0; i<edge.length;i++) {
int start = edge[i][0];
int end = edge[i][1];
graph[start].add(end);
graph[end].add(start);
}
for(LinkedList li : graph) {
System.out.println(li);
}
int[] count=new int[n+1];//1과의 거리 저장
boolean[] visited=new boolean[n+1];//방문여부
Queue<Integer> q=new LinkedList<>();
q.add(1);//시작점
visited[0]=visited[1]=true;//1에서 시작(0은 사용안함)
int now;
while(!q.isEmpty()){
now=q.poll();
for(int v: graph[now]){//나와 연결된 노드들
if(!visited[v]){//방문하지 않은 곳이라면
count[v]=count[now]+1;//1과의 길이 저장
visited[v]=true;
q.add(v);//이곳과 연결된 노드에 방문하기 위함
}
}
}
//System.out.println(Arrays.toString(count));
int max=0;//1과 가장 멀리 떨어진 노드와의 길이 저장
for(int cnt:count){
if(max<cnt){//더 큰 길이가 있다면 그게 max
max=cnt;
answer=1;
}
else if(max==cnt) answer++;
}
return answer;
}
느낀점
1. 문제를 자세히 읽어보자.
2. 최단경로를 사용한다고 하면 BFS를 사용하자.
'코딩일기 > 알고리즘' 카테고리의 다른 글
| [프로그래머스 : 레벨 3] 순위 : 플로이드워셜 알고리즘(Java) (0) | 2021.07.09 |
|---|---|
| [자료구조] 플로이드 워셜 알고리즘 (Java) (0) | 2021.07.09 |
| [프로그래머스 : 레벨 4] 징검다리 : 이분탐색(Java) (0) | 2021.07.02 |
| [프로그래머스 : 레벨3] 입국심사 : 이분탐색(Java) (0) | 2021.06.30 |
| [자료구조] 이분(이진)탐색 트리 구현 (Java) (0) | 2021.06.29 |
